Map to the Mandelbrot northernmost point

update: there are points a very tiny bit more northernmost than my point, more below the images. Iterating f(x)=x2+c, if we take c as
Robert Munafo's northernmost point, we can see that perhaps this point, is the point where f^14(0)=-f^1(0),f^15(0)=f2(0), where c approx -0.207107867093967+1.122757063632597i which leads to f^n(0) repeating with a period of 13, after the preperiod. Then the point c is one of the zeros of the polynomial with 2^13 terms. It is the solution nearest that point. We numerically estimate the zero iterating with Newton's method, since the polynomial is too large to work with. The result is printed to 60 decimal digits. Because this solution eventually repeats, by definition the point never escapes to infinity so it is a member of the Mandelbrot set. Such preperiodic points are called Misiurewicz points, and are algebraic numbers.
c=-0.207107867093967732893764544285894983866865721506089742782655 + 1.12275706363259748461604158116265882079904682664638092967742i

Each of the images below shows the northernmost imaginary supremum tip of the Mandelbrot set, which is conjectured to be the Misiurewicz point at c. This represents an infinite sequence of images centered vertically on the branch points, whic are also Misiurewicz points, showing the map of the path to the northernmost Misiurewicz as you go down or to the right. The sequence of branch Misiurewicz points have a pre-periods of n, before repeating with period=1. Each image is cenetered vertically on a three way branch Misiurewicz point, and shows the winding path from that Misiurewicz point to the northernmost Misiurewicz point. Each row has three images. The image on the left is n, and the image in the center is n+13, and n+26 is on the right. The image in the center is magnified about 10^6 more than the image on the left, and the image on the right is mangified about 10^12 more then the image on the left. Going down, each image is the next Misiurewicz point in the sequence, which is usually about 3x-5x closer to the tip than the image above it. Values of (n mod 13)=2,6,10 are skipped since they are not on the main path to the northernmost point, so the pattern has only 10 rows, instead of 13 rows. Vertically, only 10 rows are required, but I show the 11th row, which repeats the 1st row, but now the center image from the 1st row is on the left of the 11th row. The self similar pattern continues infinitely going to the right. Each row shows a sequence of self-similar images which get asymotptically more self similar as you go down the row, or to the right, which brings you closer to the northernmost point. As you go down or to the right, mini-Mandelbrots get arbitrarily small, but they are always there if you zoom in far enough. The conjectured top point is a Misiurewicz point, and all Misiurewicz points have asymptotic self similarity with an infinite number of other Misiurewicz points in the neighborhood of the point. Therefore, the approximately 10^6 scale factor going from left to right should be a constant. What is unique about this particular sequence of self similar imaages, is that there appears to be no rotation going from left to center to right, which if it were true, could be used to prove that the Misiurewicz point in question is the Mandelbrot imaginary supremum. You can click on any image for a larger view.

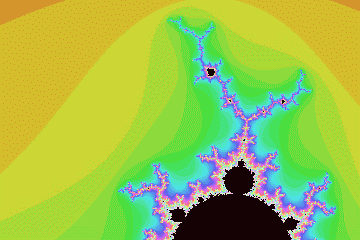
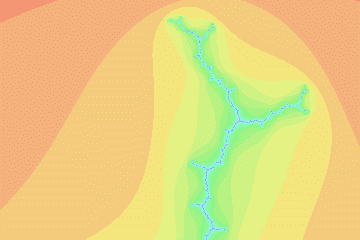
mandel03 Misiurewicz preperiod 3, period 1, imag magnification 2.61176888	mandel16 Misiurewicz preperiod 16, period 1, imag magnification 2688517.75	mandel29 Misiurewicz preperiod 29, period 1, imag magnification 2.70142518 E12
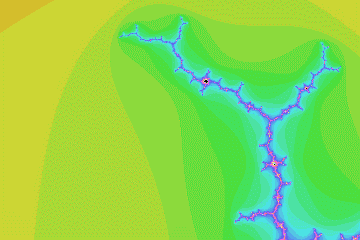
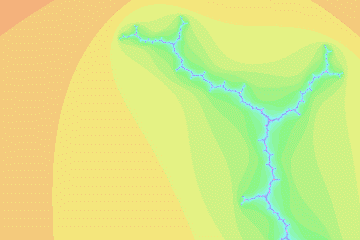
mandel04 Misiurewicz preperiod 4, period 1, imag magnification 12.0330959	mandel17 Misiurewicz preperiod 17, period 1, imag magnification 12266468.1	mandel30 Misiurewicz preperiod 30, period 1, imag magnification 1.23438673 E13
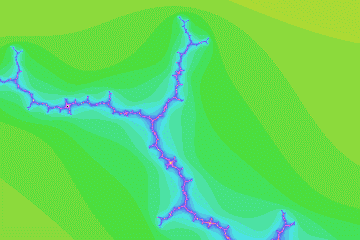
mandel05 Misiurewicz preperiod 5, period 1, imag magnification 44.9469137	mandel18 Misiurewicz preperiod 18, period 1, imag magnification 45508516.1	mandel31 Misiurewicz preperiod 31, period 1, imag magnification 4.55308861 E13
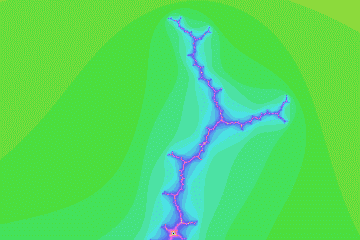
mandel07 Misiurewicz preperiod 7, period 1, imag magnification 171.562948	mandel20 Misiurewicz preperiod 20, period 1, imag magnification 172696698.	mandel33 Misiurewicz preperiod 33, period 1, imag magnification 1.73379000 E14
mandel08 Misiurewicz preperiod 8, period 1, imag magnification 757.183928	mandel21 Misiurewicz preperiod 21, period 1, imag magnification 761599024.	mandel34 Misiurewicz preperiod 34, period 1, imag magnification 7.65605902 E14
mandel09 Misiurewicz preperiod 9, period 1, imag magnification 3247.56470	mandel22 Misiurewicz preperiod 22, period 1, imag magnification 3.24786788 E9	mandel35 Misiurewicz preperiod 35, period 1, imag magnification 3.24742018 E15
mandel11 Misiurewicz preperiod 11, period 1, imag magnification 11220.8914	mandel24 Misiurewicz preperiod 24, period 1, imag magnification 1.12621405 E10	mandel37 Misiurewicz preperiod 37, period 1, imag magnification 1.13030374 E16
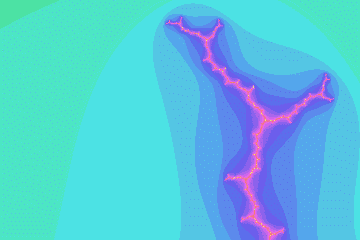
mandel12 Misiurewicz preperiod 12, period 1, imag magnification 46969.3590	mandel25 Misiurewicz preperiod 25, period 1, imag magnification 4.72588372 E10	mandel38 Misiurewicz preperiod 38, period 1, imag magnification 4.75518957 E16
mandel13 Misiurewicz preperiod 13, period 1, imag magnification 208491.433	mandel26 Misiurewicz preperiod 26, period 1, imag magnification 2.10108284 E11	mandel39 Misiurewicz preperiod 39, period 1, imag magnification 2.11750964 E17
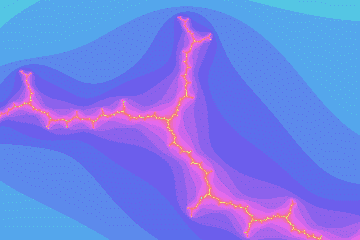
mandel14 Misiurewicz preperiod 14, period 1, imag magnification 648404.820	mandel27 Misiurewicz preperiod 27, period 1, imag magnification 6.49199324 E11	mandel40 Misiurewicz preperiod 40, period 1, imag magnification 6.50011502 E17
mandel16 Misiurewicz preperiod 16, period 1, imag magnification 2688517.75	mandel29 Misiurewicz preperiod 29, period 1, imag magnification 2.70142518 E12	mandel42 Misiurewicz preperiod 42, period 1, imag magnification 2.71449226 E18

update: there are points a very tiny bit more northernmost, by about 1.68*10^-98 further north than my point. Consider row 13,26,39, 13n... extended to infinity. There is a very tiny counterclockwise rotation of approximately 1 part in 200, each time you go to the right. In the limit, the magnification factor going from one column to the next is the inverse of the scale factor, and is is 1001821.04 - 5256.41697i. If you'll notice this particular row 13n, you can see that if you rotate it counterclockwise just enough, than the foot on the right becomes more northernmost than my Misiurewicz point. The directions on the "map" to the northernmost point are correct until the 16th column of the 13n row; where the northernmost point requires turning right instead of turning left! c1 is my oritinal no longer northernmost Misiurewicz point, printed accurate to 105 decimal digits, and c2 is a very slightly more northernmost point, approximately 1.68*10^-98 farther north, generated from that right turn in the 16th column of the 13n row. Wow! The recipe for generating this second point is that it has a period of 199, after a preperiod of 1, generated using Newton's method. Of course, you have to get very close to the point before Newton's method will converge. And also, of course, this is not "the" northernmost point either...
c1= -0.207107867093967732893764544285894983866865721506089742782655437797926445872029873945686503449818426679850 + 1.12275706363259748461604158116265882079904682664638092967742378016679413783606239593843344659123247751651i
c2= -0.207107867093967732893764544285894983866865721506089742782655437797926445872029873945686503449815177663235 + 1.12275706363259748461604158116265882079904682664638092967742378016679413783606239593843344659123249431573i


mandel208

This image magnified 2.08536683*10^95; In this row 13n, column 16 image, the path to the northernmost point requires turning right instead of left. The almost northernmost point c1 lies on the repeating path to the left, whereas the point c2 lies on the path to the right.